Sampling merupan suatu metode pencuplikan atau pengambilan nilai dengan periode konstan sesuai dengan frekuensinya. Dapat dikatakan kita mengambil sinyal pada waktu tertentu yang memiliki waktu tertentu tetapi dengan periode yang sama, dalam hal ini sinyal yang dihasilkan adalah sebuah sinyal diskrit
Sinyal kontinu disampling menjadi sinyal digital
Sebelum masuk kesampling maka kita perlu tau tentang konsep frekuensi.
1. Sinyal sinusoidal waktu kontinu
t = waktu
A = amplitude
OMEGA = frekuensi sudut[radian/detik]
q = fasa [radian]
A = amplitude
OMEGA = frekuensi sudut[radian/detik]
q = fasa [radian]
F= frekuensi (Hz)
2. sinyal sinusoidal waktu diskrit
n = bilangan bulat (integer)
A = amplituda
w = frekuensi [radian/sampel]
q = fasa [radian]
f= frekuensi (radian)
kemudian untuk sampling ada tiga pokok yaitu amplitudo, frekuensi, dan sudut (fasa). Sebagai contoh :
kita memiliki sinyal kontinu
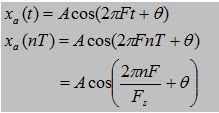
Persamaan di atas dapat dipersingkat menjadi
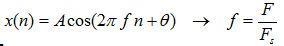
Fs = frekuensi sampling
T =sampling iterval
Untuk memudahkan kita menganalisinya kita menggunakan matlab. Kita akan menganalisis menggunakan 2 buah sinyal dengan frekuensi masing-masing 10 Hz dan 50 Hz, dengan t (waktu) 0 sampai 2 detik dengan interval waktu 0.001 detik.
Program 1.
>> f1=10; //frekuensi 1
>> f2=50; // frequensi 2
>> t=[0:0.001:2/f1];
>> x1t=cos(2*pi*f1*t);
>> x2t=cos(2*pi*f2*t);
>> figure;subplot(2,1,1);plot(t,
Bentuk sinyalnya yang terbentuk akan seperti gambar di bawah ini:
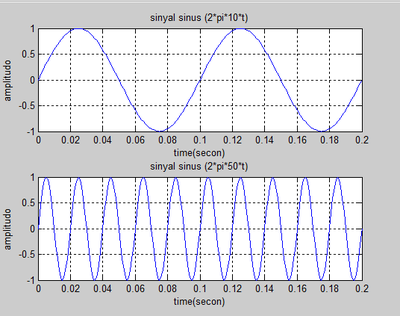
Dari gambar tersebut kita dapat menganalisis jika frekuensinya lebih besar maka panjang gelombangya semakin besar. Dari sinyal tersebut kemudian kita sampling dengan frekuensi sampling (Fs) = 40 Hz, dengan rumus
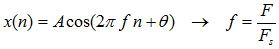
Perhitungannya berarti
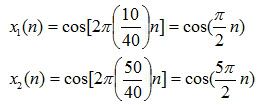
Program 2. Melakukan sampling dari sinyal di atas
f1=10;
f2=50;
x1t=cos(2*pi*f1*t); //frekuensi yang disampling
x2t=cos(2*pi*f2*t);
Fs=40; //frequensi sampling
nxTs=0:1/Fs:max(t); // pannjang waktu
xt2_nT=cos(2*pi*f2*nxTs); //frequensi yang telah di sampling
xt1_nT=cos(2*pi*f1*nxTs);
figure;subplot(2,1,1);plot(t,
sinyalnya adalah
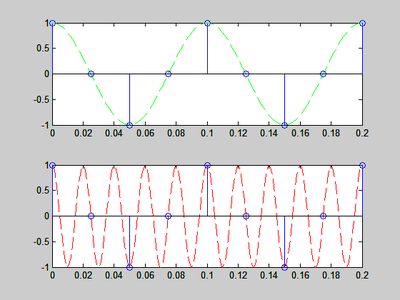
Dari gambar di atas, sinyal yang pertama merupakan sinyal berfrekuensi 10 Hz disampling dengan frekuensi sampling 40 Hz, sehingga memiliki periode 1/40. Jadi program ini akan mengambil nilai sinyal dari representasi sinyal sinusoidal berfrequensi 10 Hz setiap 1/40 detik. Sinyal yang berwarna hijau adalah sinyal kontinu yang belum di sampling. Kemudian hasil samplingnya itu adalah direpresentasikan berwarna biru.
Kemudian gambar yang kedua adalah gambar di bwahnya yang merupakan representasi dari sinyal sinusoidal berfrekuensi 40 Hz, di sampling dengan frekuensi sampling 40 Hz, sehingga dapat dihitunf periodenya yaitu 1/40 second. Sinyal yang berwarna hijau adalah sinyal kontinu yang belum di sampling. Sedangkan hasil samplingnya itu adalah direpresentasikan dengan berwarna biru.
Jika frekuensi sampling di perbesar akibatnya adalah pengambilan sampel semakin banyak hal ini dikarnakan periode samplingnya semakin kecil. Sebaliknya jika frekuensi sampling di perkecil akibatnya adalah pengambilan sampel menjadi lebih sedikit karena periodenya besar.
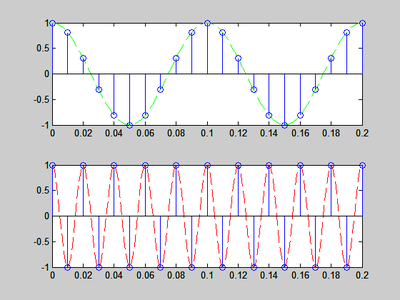
Berikut ini adalah program dengan frekuensi sampling 100 Hz :
Fs=100;
nxTs=0:1/Fs:max(t);
xt2_nT=cos(2*pi*f2*nxTs);
xt1_nT=cos(2*pi*f1*nxTs);
figure;subplot(2,1,1);plot(t,
representasi sinyalnya adalah




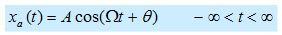
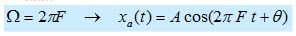
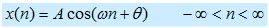
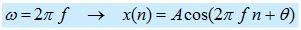
Tidak ada komentar:
Posting Komentar