Metode transformasi ada dua macam yang pertama adalah Transformasi Fourier Waktu Diskrit (Discret-Time Fourier Transform) dan discrete fourier transform.
Pada praktikum kali ini kita belajar untuk merepresentasikan metode yang pertama yaitu transformasi fourier waktu diskrit.
Sebelum kita merepresentasikan dalam matlab terlebih dahulu kita pahami definisi dari transformasi fourier waktu diskrit.
Transformasi fourier waktu diskrit adalah suatu representasi skuen eksponensial kompleks ( e^-jw) dimana w adalah variabel frekuensi real.Transformasi fourier waktu diskrit waktu diskrit ( e^-jw) dari sebuah skuen x(n) di definisikan :
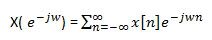
Dimana X( e^-jw) adalah sebuah fungsi kompleks yang memiliki bagian real , imajiner, magnitude dan fasa. Dapat disimpulkan bahwa x( e^-jw) adalah jumlah dari tiap titik frekuensi yang terjadi.
Misalnya :
Kita punya x=[0.5,1,0.5]; dan n=[ 0, 1, 2];
Berarti nilai dari X( e^-jw) adalah X=0.5*e^-jw0 + 1*e^-jw*1 + 0.5*e^-jw*2; sepanjang -pi<=w<=pi
Untuk mempermudah kita dalam menganalisis sinyal waktu diskrit didasarkan pada transformasi fourier waktu diskrit kita gunakan fungsi didalam mathlab. Berikut ini adalah source code programnya.
>> x=[0.5,1,0.5];
>> n=[0:2];
>> w= -pi:0.01:pi;
>> X= 0.5+exp(-j*w*1) + 0.5*exp(-j*w*2);
>> figure;subplot(4,1,1); plot(w,abs(X));xlabel('freq sudut');ylabel('magnitude');
subplot(4,1,2); plot(w,angle(X));xlabel('freq sudut');ylabel('Phase');
subplot(4,1,3); plot(w,real(X));xlabel('freq sudut');ylabel('real');
subplot(4,1,4); plot(w,imag(X));xlabel('freq sudut');ylabel('imaginare');
kita menggunakan fungsi :
Real = untuk mengambil figure dari nilai realnya
Imag = untuk mengambil figur yang bilangan imaginer
Abs = untuk memperlihatkan magnitudenya
Angle = untuk memperlihatkan sudutnya (fasa)
>> x=[0.5,1,0.5]; = ini adalah nilai sepanjang indeks ke- n dimana 0<= n <=2
>> w= -pi:0.01:pi; = sebagai indeks untu tiap sampel frekuensi. Dari – pi sampai pi, kita juga dapat merubahnya dari -3pi sampai dengan 3pi. Lebih besar rangenya Nanti akan berpengaruh terhadap periodic sinyal yang dihasilkan.
>> X= 0.5 + exp(-j*w*1) + 0.5*exp(-j*w*2); = merupakan hasil dari penjumlahan tiap titik-titik frekuensi yang terbentuk.
Untuk menampilkan representasi dari sinyal yang terbentuk kita gunakan fungsi
>> figure;subplot(4,1,1); plot(w,abs(X));( untuk magnitudenya)
subplot(4,1,2); plot(w,angle(X)); (untuk fasanya)
subplot(4,1,3); plot(w,real(X)); (untuk representasi bilangan real-nya)
subplot(4,1,4); plot(w,imag(X)); (untuk representasi bilangan imaginernya).
Dari contoh di atas menghasilkan gmbar seperti dibawah ini
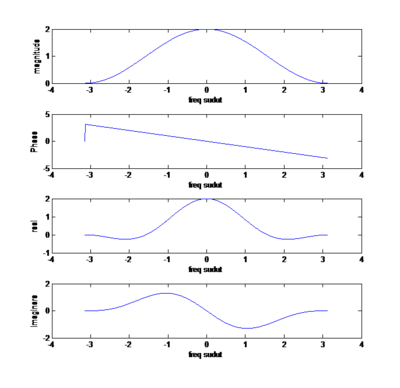
Gambar 1 untuk w= -pi : 0.01: pi
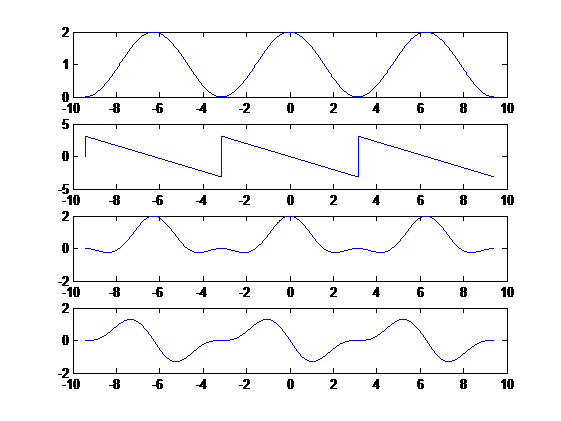
Gambar 2 untuk w= -3pi : 0.01: 3pi
Program diatas masi terdapat kekurangan, dimana jika kita ingin melakukan transformasi sepanjang 256 sampel. Apa kita harus manual untuk menjumlahkannya. Tentu saja tidak, dengan mathlab sudah disediakan untuk melakukan penjumlahaan deret yang memiliki pola tertentu yaitu dilakukan dengan menggunakan perulangan for.
Sebelum kita membuat fungsinya terlebih dahulu kita analisi pola penjumlahanya. Kita punya nilai x = 0.5, 1, 0.5 , dan n = 0,1,2 penjumlahannya X=0.5*e^-jw0 + 1*e^-jw*1 + 0.5*e^-jw*2;
Jika kita ingin mengakses nilai 0.5 maka letaknya adalah x(1), nilai 1 letaknya x(2), nilai 0.5 letaknya x(3). Berarti jika kita ingin mengakses nilai a di suatu deretan x letaknya adalah a=x(k). begitu juga nilai n, jika kita ingin mengakses nilai 0 maka letaknya x(1), nilai 1 letaknya x(2) dan nilai 2 letaknya x(3), untuk nilai b di n diurutan k maka letaknya n(k);
Maka penjumlahan tersebut dapat diubah dalam bentuk fleksibel atau umum menjadi
X= X + x(k)*e^-j*w*n(k);
Dan penjumlahan tersebut di looping sebanyak N, dimana N adalah panjang dari indeks deret sinyal.
Untuk fungsinya seperti berikut ini :
function[Xe]=DTFT(x,n)
w=-3*pi:0.01:3*pi;
Xe=0;
for k=1:length(x)
X=x(k)*exp(-j*w*n(k));
k=k+1;
Xe=Xe+X;
end
figure;subplot(4,1,1); plot(w,abs(Xe)); xlabel('frequensi sudut');ylabel('Magnitude');
subplot(4,1,2); plot(w,angle(Xe));xlabel('
subplot(4,1,3);plot(w,real(Xe)
subplot(4,1,4); plot(w,imag(Xe)); xlabel('frequensi sudut');ylabel(Imaginer');
Penjelasan :
- K adalah indeksing untuk perulangan sampai sepanjang length(x) atau length (n);
- K= k+1 adalah untuk pertambahan satu angka sehingga k selalu bertambah
- Xe adalah untuk menampung nilai penjumlahan dari X yang berubah setiap perulangan
- Figure; untuk merepresentasikan dalam bentuk gambara/
- Subplot(4,1,2); untuk menempatkan gambar dalam satu bingkan dimana angka 4 menunjukkan banyak baris, 1 menunjukkan jumlah kolom, dan 2 menunjukkan posisi gambar. Dimana nilai-nilai ini dapat kita modifikasi sesuai keinginan
- Abs, angle, real, imag sudah diterangkan di depan.
Contoh :
Kita punya x=[ones(1,4)]; dan n=[1:4];
Kemudian kita panggil fungsi yang telah kita buat tadi dan disimpan dengan nama DTFT. Panggil fungsinya dengan DTFT(x,n);
Dan hasil sinyalnya adalah seperti berikut ini :
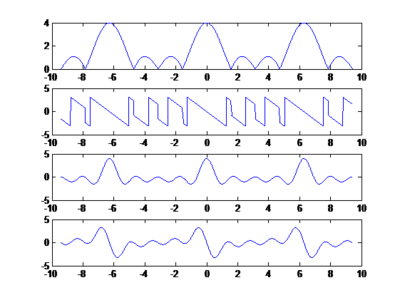




Tidak ada komentar:
Posting Komentar