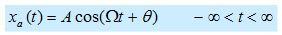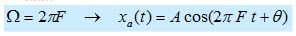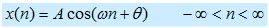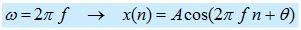MEMBUAT APLIKASI DENGAN GUI MATLAB (GUI BUILDER)

Bismillah, Assalamualaikum . .

Berikut ini adalah akan saya bahas mengenai hasil praktikum pengolahan sinyal digital pada pukul 15.00 tanggal 13-November-2012. Pada praktikum kali ini adalah mencoba untuk membuat GUI di MATLAB menggunakan GUIDE (GUI Builder). Dengan harapan ketika sebuah program dibuat GUI (Graphical User Interface) lebih mudah dipelajari dan digunakan, karena user tidak tahu apa yang sebenarnya program ini lakukan ketika program ini deksekusi. Dengan GUI ini akan mempermudah orang lain dalam menggunakan aplikasi buatan kita, sedangkan pada tahap pembuatannya yang lumayan susah. GUIDE atau GUI builder merupakan sebuah graphical user interface (GUI) yang dibangun dengan
obyek grafik seperti tombol (button), kotak teks, slider, menu dan lain-lain.

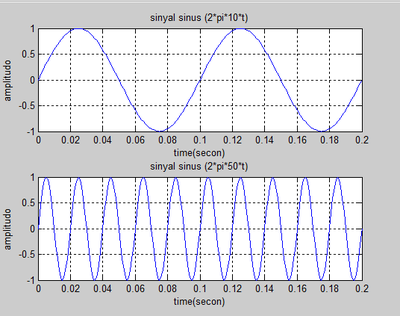
Pada kali ini kita akan membuat sebuah aplikasi dari matlab untuk penghitungan sinyal sinus dan cosinus. Dimana program ini akan menghitung dan menampilkan hasil representasi dari sinyal sinus dan cosinus yang dihasilkan dalam bentuk gelombang.

langkahnya adalah sebagai berikut ini :

1. Untuk memulainya ada 2 cara , yang pertama menggunakan command line dengan mengetikkan >> guide, yang kedua dengan mengklik tombol Start Matlab -> Matlab -> GUIDE (GUI Builder).

Gambar 1. GUIDE Quick Start

GUIDE Quick Start memiliki dua buah pilihan, yaitu Create New GUI dan Open Existing GUI. Create New GUI digunakan jika kita memang belum pernah membuat aplikasi GUI Matlab atau jika kita memang ingin membuat sebuah figure baru, sedangkan Open Existing GUI digunakan jika kita akan memodifikasi file figure yang telah kita simpan atau sudah kita buat sebelumnya.

Kemudian jika kita memilih Creat New GUI maka kita akan diberikan suatu halaman untuk membuat tampilan dari program yang akan kita buat. Yang nantinya akan tampil seperti berikut ini

Gambar 2. Tampilan Menu bar

Di atas merupakan menu-menu utama yang nantinya kita gunakan untuk membuat program berbasis GUI dari matlab. Alignment tool digunakan untuk mengatur posisi dari menu menu yang telah kita buat agar terlihat rapi dan sejajar. Component Pallete digunakan untuk membuat tampilan menu pada program yang kita akan buat. Layout Editor digunakan untuk lembar kerja kita membuat tampilan program kita. Menu Editor digunakan untuk mengedit menu program kita. M-file Editor digunakan untuk mengedit program melalui source code program yang sedang dibuat. Property Inspector menu yang digunakan untuk mengatur properti dari masing-masing kontrol. Run digunakan untuk mengeksekusi program atau menjalankan program yang sedang kita buat.

Gambar 3. Menu Pallete

Menu pallete diatas kegunannya untuk membuat menu-menu dalam program matlab yang kita buat. Yang pertama ada Push Button digunakan untuk membuat menu yang berfungsi sebaga tombol atau switch. Radio Buttondigunakan untuk membuat menu yang hanya dipilih salah satu menu saja. Edit Text digunakan untuk membuat menu yang digunakan untuk menerima inputan dari user dalam artian dapat diubah oleh user. Slider merupakan menu yang digunakan untuk membuat inputan bukan dari keyboard tapi dari pergeseran, menggesernya hanya dapat dua arah yaitu vertical dan horizontal. Group Menu / list Box adalah menu yang digunakan untuk mengelompokkan menu dalam satu frame pada keselurruhan menu. Axes digunakan untuk menampilkan sebuah grafik atau gambar (image). Axes sebenarnya tidak masuk dalam UIControl, tetapi axes dapat diprogram agar pemakai dapat
berinteraksi dengan axes dan obyek grafik yang ditampilkan melalui axes. Toggle Button hampir sama dengan push button yang membedakan adalah jika kita menggunakan push button maka ketika di klik tombol akan kembali kesemula pada Toggle Button ini dia tidak akan kebal kebentuk semula. Check Box digunakan untuk membuat menu pilihan yang dapat dipilih lebih dari satu. Static Text kegunaanya adalah untuk memberi label pada menu tertentu. Frame merupakan kotak yang digunakan untuk mengelompokkan kontrol-kontrol dari semua program kita. Popup Menu digunakan untuk Popop menu berguna menampilkan daftar pilihan yang didefinisikan pada String Propoerty ketika mengklik tanda panah pada aplikasi dan memiliki fungsi yang sama seperti radio button.

2. Setelah kita mengetahi dasarny kemudian kita mencoba untuk membuat program kita. Caranya adalah Seperti yang pertama ketikkan di command linde >> guide [enter]. Kemudian buat halaman kerja baru dan di save dengan nama Program GUI pertama.

a. Mendesain figure menuPada desain ini kita membuat sutu program kontrol-kontrol yang dibutuhkan itu apa saja. Pada program yang akan kita buat adalah kita membutuhkan input berupa pilihan sinus ataupun cosinus, inputan amplitudo, frekuensi, dan fasa. Serta 3 buath tombol untuk untuk kontrol program dan satu buah axes untuk menampilkan representasi berupa gambar grafik. Dari kontrol-kontrol yang dibutuhkan kita membutuhkan 2 buah radio button, 3 buahEdit text untuk menerima inputan Amplitudo, Frekuensi, dan fasa, 3 buah Push Button, 1 buah axes untuk tampilan, 1 buah Button Group. Untuk desain saya adalah seperti berikut

Gambar 4. Desain tampilan program

b. Mengatur property masing-masing kontrolSetelah kita mendesain tampilan menunya kita atur masing-masing kontrol dengan menggunakan property inspector.

Komponen	Property Inspector
	Font Size	String	Tag
Radio Button1	12	Sinus	sinus
Radio button 2	12	Cosinus	cosinus
Edit text 1	12	null	edit1
Edit text 2	12	null	edit2
Edit text 3	12	null	edit3
push button1	12	Execute	ExecuteProgram
push button2	12	Reset	reset
push button3	12	Quit	Exit
axes			axes1

c. Mengatur syntaxs programAgar program kita berjalan seperti yang kita harapkan yang terpenting adalah mengedit source code dari program kita agar fungsi-fungsi seperti reset, execute, exit dll dapat bekerja sesuai harpankita. caranya adalah dengan mengatur pada call back masing-masing kontrol.

caranya adalah dengan mengklik kanan pada komponen yang ingin kita beri fungsi view callback -> callback

• Sinus
  Di fungsi sinus kita tambahkan kode berikut
  set(handles.cosinus,'Value',0);
  pilih = 1;
  handles.pilih=pilih;
  guidata(hObject,handles)
• cosinus
  Pada Cosinus juga ditambahkan kode yang hampir sama dengan nomer 1,
  set(handles.sinus,'Value',0);
  pilih = 2;
  handles.pilih=pilih;
  guidata(hObject,handles)
• ExecuteProgram
  untuk menghitung nilai yang dihasilkan Pada fungsi ini ditambahkan kode berikut :
  A=str2num(get(handles.edit1, 'string')); %mengambil nilai pada edit1
  F=str2num(get(handles.edit2, 'string')); %mengambil nilai pada edit2
  theta=str2num(get(handles.edit3, 'string')); %mengambil nilai pada edit3
  t=-3/F:1/50/F:3/F; %membangkitkan sumbu t
  
  pilih=handles.pilih %berhubungan dg pilihan pada radiobutton
  switch handles.pilih
  case 1 %jika radiobutton1 yang ditekan
  y=A*sin(2.*pi.*F.*t+theta); %maka menghitung nilai sinus
  case 2 %jika radiobutton2 yang ditekan
  y=A*cos(2.*pi.*F.*t+theta); %maka menghitung nilai cosinus
  end
  
  axes(handles.axes1); %ditampilkan ddi axes1
  a=0; %membuat garis, seperti sumbu x dan sumbu y
  plot(t,y,'r'); %menampilkan hasil perhitungan
  xlabel('detik');ylabel('Amplitudo');
  xlim([min(t) max(t)]);
  grid on
• reset
  untuk mereset seperti pada awal program dijalankan, caranya adalah mengosongkan masing-masing inputan. Yang string dibuat null dan yang berisi value di beri nilai 0
  set(handles.edit1 , 'string', ''); %mengosongkan string pada edit1
  set(handles.edit2, 'string', ''); %mengosongkan string pada edit2
  set(handles.edit3, 'string', ''); %mengosongkan string pada edit2
  set(handles.cosinus,'Value',0);
  set(handles.sinus,'Value',0);
  axes(handles.axes1);
  plot(0);
• exit
  untuk keluar program kita tambahkan fungsi close();

d. Run Program 
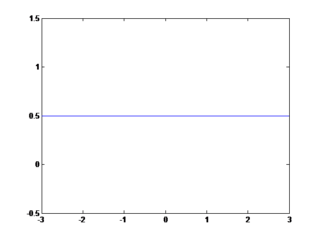
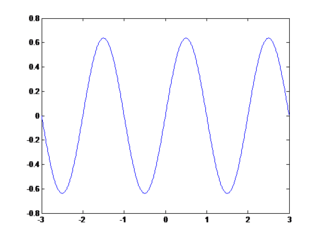
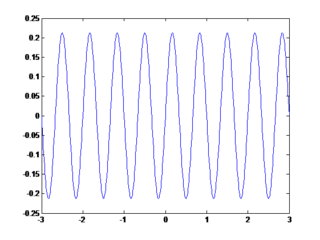
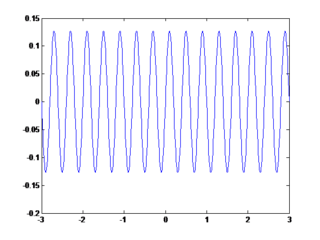
Setelah semuanya selesai kemudian kita Run program dengan cara mengklik tombol RUN, setelah itu kita coba isikan nilainya apakah program berjalan dengan baik. jika belum maka di perbaiki lagi sampai hasilnya seperti ini :

Gambar 5. Hasil akhir

Lanjut baca - MEMBUAT APLIKASI DENGAN GUI MATLAB (GUI BUILDER)

Lanjut Sampling dan Aliasing (Efect Niquyst)

SAMPLING dan ALIASING

kemarin kita sudah belajar mengenai sampling pada kali ini kita akan belajar bagaimana kita menyampling suatu sinyal digital, apa pengaruhnya penggunaan frekuensi sampling pada sinyal digital berikut ini adalah uraian yang dapat saya sampaikan pada analisis sampling dan aliasing.

1.       Pengamatan Pengaruh Pemilihan Frekuensi Sampling Secara Visual

Pada praktikum kali ini kita akan mengamati tentanga sampling dan aliasing, dimana kita tahu bahwa untuk mengkonversi dari sinyal analog ke digital memerlukan beberapa proses, yakni sampling, kuantisasi dan coding. Selain itu untuk mengkonversi sinyal digital ke analag juga memerlukan proses digital konversi.

Pertama kita lakukan pada praktikum kali ini adalah mengamati pengaruh frekuensi sample yang berbeda untuk setiap periode sinyal. Untuk membuat sinyal di gital sinusoidal adalah seperti program di bawah ini

Fs=8;%frekuensi sampling

t=(0:Fs-1)/Fs;%proses normalisasi

s1=sin(2*pi*t*2);

subplot(211)

stem(t,s1)

axis([0 1 -1.2 1.2])

Fs=16;%frekuensi sampling

t=(0:Fs-1)/Fs;%proses normalisasi

s2=sin(2*pi*t*2);

subplot(212)

stem(t,s2)

axis([0 1 -1.2 1.2])

dari program di atas frekuensi sampling yang lebih besar menghasilkan sampling yang lebih banyak dari pada program sinyal sinusoidal yang memiliki frekuensi sampling yang lebih sedikit. Program di atas gambarnya seperti berikut :

Gambar 1 perbedaan jumlah frekuensi sampling

2.       Pengamatan Pengaruh Pemilihan Frekuensi Sampling pada Efek Audio

Setelah kita mengetahui bahwa pengaruh jumlah frekuensi sampling akan menghasilkan jumlah nilai samplingan yang berbeda secara visual, sekarang kita akan mendengarkan bagaimana pengaruh frekuensi sampling melalui sinyal audio.

Kita membuat file di editor baru dan mengetikkan program berikut :

clear all;

Fs=1000;

t=0:1/Fs:0.25;

f=100;

x=sin(2*pi*f*t);

sound(x,Fs)

fungsi ini digunakan untuk memperdengarkan sinyal sampling sin, dalam bentuk sebuah suara. Dimulai dengan perintah clear all yang berfungsi menghapus semua data yang ada di dalam workspace. Kemudian menentukan frekuensi sample yang di dalam contoh itu sebesar 10000. Dan juga menentukan t yang berfungsi sebagai pedoman seberapa lama nada itu berakhir. Kemudian menentukan besarnya frekuensi yang dalam hal ini besarnya adalah 100. Dan kemudian membuat persamaan sinyal sinus x=sin(2*pi*f*t). dan terakhir adalah keyword sound yang digunakan untuk mengirim bunyi dari vektor x dengan frekuensi sampling Fs ke speaker.

Jika program dijalankan terdapat suara yang muncul pada waktu t. Kemudian kita ubah f menjadi 200 sampai 900. Hasilnya adalah ada perubahan tinggi nada yang dihasilkan kemudian kembali merendah seperti pada nada sebelumnya. Yaitu nada yang dihasikan frekuensi 100 sama dengan frekuensi 900, frekuensi 200 sama dengan frekuensi  800, frekuensi 300 sama dengan frekuensi  700, frekuensi 400 sama dengan frekuensi  600.

Dapat disimpulkan bahwa sinyal Frekuensi 100 alias 900, Frekuensi 200 alias 800, Frekuensi 300 alias 700, Frekuensi 400 alias 600.

Suara akan tetap dihasilkan selama besar f< 2Fs. Jadi sinyal 1000 tidak dapat dihasilkan melalui program di atas.

3.       Pengamatan Efek Aliasing pada Audio 1

Kali ini kita akan membuat beberapa nada dengan frekuensi yang berdebeda, dari situ kita dapat membuat rangkaian nada tersebut menjadi sebuah lagu yang enak di dengar. Untuk itu kita buat contoh program untuk menganalisis bagaimana pengaruh frekuensi sampling pada efek aliasing dengan menyusun sebuah nada menjadi rangkaian lagu. Dibawah ini merupakan program yang akan kita analisis

clc

Fs=3000;

t=0:1/Fs:0.25;

c=sin(2*pi*262*t);

d=sin(2*pi*294*t);

e=sin(2*pi*330*t);

f=sin(2*pi*249*t);

g=sin(2*pi*392*t);

a=sin(2*pi*440*t);

b=sin(2*pi*494*t);

c1=sin(2*pi*523*t);

nol = [zeros(size(t))];

nada1 = [c,e,c,e,f,g,g,nol,b,c1,b,c1,b,g,nol,nol];

nada2 = [c,e,c,e,f,g,g,nol,b,c1,b,c1,b,g,nol];

nada3 = [c,nol,e,nol,g,nol,f,f,g,f,e,c,f,e,c,nol];

nada4 = [c,nol,e,nol,g,nol,f,f,g,f,e,c,f,e,c];

lagu=[nada1,nada2,nada3,nada4];

sound(lagu,Fs);

wavwrite(lagu,'gundul.wav');

Fungsi diatas digunakan untuk membuat nada-nada yang kemudian akan disusun menjadi sebuah lagu dalam format wav. Prinsip dari fungsi kedua ini sama dengan fungsi yang pertama. Jadi yang dilakukan adalah mengirimkan sinyal di vektor not (c,d,e,f,g,a,b,cl) yang disampling oleh Fs. kemudian not not itu disusun dalam matriks nada (nada1,nada2,nada3,nada4). Nada-nada itu kemudian disatukan kedalam sebuah matriks lagu yang akan dikirim ke speaker oleh keyword sound. Terakhir dengan keyword wavwrite akan menuliskan ke dalam file .wav, yang bisa di dengarkan di pemutar lain.

Kemidian kita merubah frekuensi sampling kita menjadi nilai frekuensi sampling Fs=16000, menjadi Fs =10000, 8000, 2000, 1000, 900, 800, 700, 600, dan 500. Semakin rendah frekuensi sampling yang ita gunakan maka suaranya semakin tidak beigitu jelas seperti yang frekuensi 16000

Kemudian kita ubah ubah frekuensi sampling dengan frekuensi sampling 2 kali lebih besar dari frekuensi yang disampling maka frekuensi sampling nada yang dihasilkan semakin tidak jelas, ada makna yang tidak tersampaikan jadi terdengar terdapat blur pada nada yang dihasilkan.

Semakin tinggi frekuensi samplingnya maka nada tersebut berbunyi lebih cepat dari nada yang sebelumnya begitu sebaliknay jika frekuensi samplingnya lebih kecil maka nada tersebut semakin lambat. Hal ini dapat dibuktikan karena semakin besar frekuensi sampling yang kita gunakan maka semakin kecil periodenya, jadi jarak antara gelombang satu dengan gelombang lain semakin merapat dan mendekat sehingga akan tercipta nada yang cepat pula dan begitu sebaliknya.

4.       Pengamatan Efek Aliasing pada Audio 2

 Kemudian kita mencoba untuk menggunakan lagu yang diambil dari sebuah file *.wav. kemudian akan disampling menggunakan beberapa frekuensi sampling. Berikut ini adalah programnya

clear all;

[Y,Fs]=wavread('LP.wav');

Fs=16000;%nilai default Fs=16000

%Pilihan untuk memainkan lainnya Fs=8000, 11025, 22050,44100

sound(Y,Fs)

fungsi ketiga ini digunakan untuk mengembalikan nilai Fs dari ‘LP.wav’ dalam herzt dan dikirim ke speaker untuk kembali dikeluarkan. Fs digunakan untuk mengatur berapa besarnya frekuensi sampling yang mau kita analisis.

Dengan frekuensi sampling  16000 Hz lagu terdengar sama seperti aslinya, sehingga kita dapat menangkap apa yang sedang berbunyi.

Kemudian kita turunkan lagi menjadi 8000 Hz namun suaranya terdengar lebih rendah dan lebih lambat temponya dari yang sebelumnya hal ini di akibatkan semakin besar frekuensi samplingnya makan semakin rapat atau semakin banyak nilai sampling yang dapat diambil.

Kemudian saya ingin mencoba kembali merubahnya dengan frekuensi sampling Fs = 11025, 22050, dan 44100.

Pada frekuensi 11025 lagu terdengar agak melambat, karena frekuensi sampling lebih kecil dari frekuensi yang di sampling sehingga suaranya sedikit melambat

Pada frekuensi 22050 lagu terdengar dipercepat, karena frekuensi sampling lebih besar dari frekuensi yang di sampling sehingga suaranya sedikit dipercepat dari lagu sebelumnya.

Pada frekuensi 44100 lagu terdengar semakin tambah cepat, karena frekuensi sampling lebih besar dari frekuensi yang di sampling sehingga suaranya semakin cepat dan ini adalah frekuensi yang paling tinggi saya gunakan kita dapat menggunakan yang lebih tinggi lagi.

Kesimpulannya semakin tinggi frekuensi sampling semakit kecil periodenya jika semakin kecil periodenya maka semakin banyak nilai yang disampling, dengan semakin banyak nilai yang disampling semakin rapat bentuk gelombangnya hasilnya semakin cepat untuk berpindah nada karena periodenya yang singkat.

Lanjut baca - Lanjut Sampling dan Aliasing (Efect Niquyst)

SAMPLING

Sampling merupan suatu metode pencuplikan atau pengambilan nilai dengan periode konstan sesuai dengan frekuensinya. Dapat dikatakan kita mengambil sinyal pada waktu tertentu yang memiliki waktu tertentu tetapi dengan periode yang sama, dalam hal ini sinyal yang dihasilkan adalah sebuah sinyal diskrit

Sinyal kontinu disampling menjadi sinyal digital

Sebelum masuk kesampling maka kita perlu tau tentang konsep frekuensi.

1. Sinyal sinusoidal waktu kontinu

t = waktu
A = amplitude
OMEGA = frekuensi sudut[radian/detik]
q = fasa [radian]

F= frekuensi (Hz)

2. sinyal sinusoidal waktu diskrit

n = bilangan bulat (integer)

A = amplituda

w = frekuensi [radian/sampel]

q = fasa [radian]

f= frekuensi (radian)

kemudian untuk sampling ada tiga pokok yaitu amplitudo, frekuensi, dan sudut (fasa). Sebagai contoh :

kita memiliki sinyal kontinu 

Persamaan di atas dapat dipersingkat menjadi

Fs = frekuensi sampling

T  =sampling iterval

Untuk memudahkan kita menganalisinya kita menggunakan matlab. Kita akan menganalisis menggunakan 2 buah sinyal dengan frekuensi masing-masing 10 Hz dan 50 Hz, dengan t (waktu) 0 sampai 2 detik dengan interval waktu 0.001 detik.

Program 1.

>> f1=10; //frekuensi 1

>> f2=50; // frequensi 2

>> t=[0:0.001:2/f1];

>> x1t=cos(2*pi*f1*t);

>> x2t=cos(2*pi*f2*t);

>> figure;subplot(2,1,1);plot(t,x1t);xlabel('Time(second)');ylabel('Amplitudo');title('Sinyal Cosinus cos(2*pi*10*t)');subplot(2,1,2);plot(t,x2t);xlabel('Time(second)');ylabel('Amplitudo');title('Sinyal Cosinus cos(2*pi*50*t)');

Bentuk sinyalnya yang terbentuk akan seperti gambar di bawah ini:

Dari gambar tersebut kita dapat menganalisis jika frekuensinya lebih besar maka panjang gelombangya semakin besar. Dari sinyal tersebut kemudian kita sampling dengan frekuensi sampling (Fs) = 40 Hz, dengan rumus 

Perhitungannya berarti

Program 2. Melakukan sampling dari sinyal di atas

f1=10;

f2=50;

x1t=cos(2*pi*f1*t); //frekuensi yang disampling

x2t=cos(2*pi*f2*t);

Fs=40; //frequensi sampling

nxTs=0:1/Fs:max(t); // pannjang waktu

xt2_nT=cos(2*pi*f2*nxTs); //frequensi yang telah di sampling

xt1_nT=cos(2*pi*f1*nxTs);

figure;subplot(2,1,1);plot(t,x1t,'--r');hold on;stem(nxTs,xt1_nT);subplot(2,1,2);plot(t,x2t,'--r');hold on;stem(nxTs,xt2_nT);

sinyalnya adalah

Dari gambar di atas, sinyal yang pertama merupakan sinyal berfrekuensi 10 Hz disampling dengan frekuensi sampling 40 Hz, sehingga memiliki periode 1/40. Jadi program ini akan mengambil nilai sinyal dari representasi sinyal sinusoidal berfrequensi 10 Hz setiap 1/40 detik. Sinyal yang berwarna hijau adalah sinyal kontinu yang belum di sampling. Kemudian hasil samplingnya itu adalah direpresentasikan berwarna biru.

Kemudian gambar yang kedua adalah gambar di bwahnya yang merupakan representasi dari sinyal sinusoidal berfrekuensi 40 Hz, di sampling dengan frekuensi sampling 40 Hz, sehingga dapat dihitunf periodenya yaitu 1/40 second. Sinyal yang berwarna hijau adalah sinyal kontinu yang belum di sampling. Sedangkan hasil samplingnya itu adalah direpresentasikan dengan berwarna biru.

Jika frekuensi sampling di perbesar akibatnya adalah pengambilan sampel semakin banyak hal ini dikarnakan periode samplingnya semakin kecil. Sebaliknya jika frekuensi sampling di perkecil akibatnya adalah pengambilan sampel menjadi lebih sedikit karena periodenya besar.

Berikut ini adalah program dengan frekuensi sampling 100 Hz :

Fs=100;

nxTs=0:1/Fs:max(t);

xt2_nT=cos(2*pi*f2*nxTs);

xt1_nT=cos(2*pi*f1*nxTs);

figure;subplot(2,1,1);plot(t,x1t,'--r');hold on;stem(nxTs,xt1_nT);subplot(2,1,2);plot(t,x2t,'--r');hold on;stem(nxTs,xt2_nT);

representasi sinyalnya adalah

Dari gambar di atas kita dapat melihat semakin besar frekuensi maka semakit banyak sinyal yang di sampling, karena periodenya semakin kecil sehingga pengambilan nilai padda sinyal dengan periode konstan semakin banyak.

Lanjut baca - SAMPLING

Transformasi Fourier Waktu Diskrit (Discret-Time Fourier Transform)

Metode transformasi ada dua macam yang pertama adalah Transformasi Fourier Waktu Diskrit (Discret-Time Fourier Transform) dan discrete fourier transform.

Pada praktikum kali ini kita belajar untuk merepresentasikan metode yang pertama yaitu transformasi fourier waktu diskrit.

Sebelum kita merepresentasikan dalam matlab terlebih dahulu kita pahami definisi dari transformasi fourier waktu diskrit.

Transformasi fourier waktu diskrit adalah suatu representasi skuen eksponensial kompleks ( e^-jw) dimana w adalah variabel frekuensi real.Transformasi fourier waktu diskrit waktu diskrit ( e^-jw) dari sebuah skuen x(n) di definisikan :

 

Dimana X( e^-jw) adalah sebuah fungsi kompleks yang memiliki bagian real , imajiner, magnitude dan fasa. Dapat disimpulkan bahwa x( e^-jw) adalah jumlah dari tiap titik frekuensi yang terjadi.

Misalnya :

Kita punya  x=[0.5,1,0.5]; dan n=[ 0, 1, 2];

Berarti nilai dari X( e^-jw) adalah X=0.5*e^-jw0 + 1*e^-jw*1 + 0.5*e^-jw*2; sepanjang -pi<=w<=pi

Untuk mempermudah kita dalam menganalisis sinyal waktu diskrit didasarkan pada transformasi fourier waktu diskrit kita gunakan fungsi didalam mathlab. Berikut ini adalah source code programnya.

>> x=[0.5,1,0.5];

>> n=[0:2];

>> w= -pi:0.01:pi;

>> X= 0.5+exp(-j*w*1) + 0.5*exp(-j*w*2);

>> figure;subplot(4,1,1); plot(w,abs(X));xlabel('freq sudut');ylabel('magnitude');

subplot(4,1,2); plot(w,angle(X));xlabel('freq sudut');ylabel('Phase');

subplot(4,1,3); plot(w,real(X));xlabel('freq sudut');ylabel('real');

subplot(4,1,4); plot(w,imag(X));xlabel('freq sudut');ylabel('imaginare');

kita menggunakan fungsi :

Real       = untuk mengambil figure dari nilai realnya

Imag      = untuk mengambil figur yang bilangan imaginer

Abs        = untuk memperlihatkan magnitudenya

Angle    = untuk memperlihatkan sudutnya (fasa)

>> x=[0.5,1,0.5]; = ini adalah nilai sepanjang indeks ke- n dimana 0<= n <=2

>> w= -pi:0.01:pi; = sebagai indeks untu tiap sampel frekuensi. Dari – pi sampai pi, kita juga dapat merubahnya dari -3pi sampai dengan 3pi. Lebih besar rangenya Nanti akan berpengaruh terhadap periodic sinyal yang dihasilkan.

>> X= 0.5 + exp(-j*w*1) + 0.5*exp(-j*w*2); = merupakan hasil dari penjumlahan tiap titik-titik frekuensi yang terbentuk.

Untuk menampilkan representasi dari sinyal yang terbentuk kita gunakan fungsi

>> figure;subplot(4,1,1); plot(w,abs(X));( untuk magnitudenya)

subplot(4,1,2); plot(w,angle(X)); (untuk fasanya)

subplot(4,1,3); plot(w,real(X)); (untuk representasi bilangan real-nya)

subplot(4,1,4); plot(w,imag(X)); (untuk representasi bilangan imaginernya).

Dari contoh di atas menghasilkan gmbar seperti dibawah ini

Gambar 1 untuk w= -pi : 0.01: pi

Gambar 2 untuk w= -3pi : 0.01: 3pi

Program diatas masi terdapat kekurangan, dimana jika kita ingin melakukan transformasi sepanjang 256 sampel. Apa kita harus manual untuk menjumlahkannya. Tentu saja tidak, dengan mathlab sudah disediakan untuk melakukan penjumlahaan deret yang memiliki pola tertentu yaitu dilakukan dengan menggunakan perulangan for.

Sebelum kita membuat fungsinya terlebih dahulu kita analisi pola penjumlahanya. Kita punya nilai x = 0.5, 1, 0.5 , dan n = 0,1,2 penjumlahannya X=0.5*e^-jw0 + 1*e^-jw*1 + 0.5*e^-jw*2;

Jika kita ingin mengakses nilai 0.5 maka letaknya adalah x(1), nilai 1 letaknya x(2), nilai 0.5 letaknya x(3). Berarti jika kita ingin mengakses nilai a di suatu deretan x letaknya adalah a=x(k). begitu juga nilai n, jika kita ingin mengakses nilai 0 maka letaknya x(1), nilai 1 letaknya x(2) dan nilai 2 letaknya x(3), untuk nilai b di n diurutan k maka letaknya n(k);

Maka penjumlahan tersebut dapat diubah dalam bentuk fleksibel atau umum menjadi

X= X + x(k)*e^-j*w*n(k);

Dan penjumlahan tersebut di looping sebanyak N, dimana N adalah panjang dari indeks deret sinyal.

Untuk fungsinya seperti berikut ini :

function[Xe]=DTFT(x,n)

w=-3*pi:0.01:3*pi;

Xe=0;

for k=1:length(x)

X=x(k)*exp(-j*w*n(k));

k=k+1;

Xe=Xe+X;

end

figure;subplot(4,1,1); plot(w,abs(Xe)); xlabel('frequensi sudut');ylabel('Magnitude');

subplot(4,1,2); plot(w,angle(Xe));xlabel('frequensi sudut');ylabel('Magnitude');

subplot(4,1,3);plot(w,real(Xe)); xlabel('frequensi sudut');ylabel('Real');

subplot(4,1,4); plot(w,imag(Xe)); xlabel('frequensi sudut');ylabel(Imaginer');

Penjelasan  :

• K adalah indeksing untuk perulangan sampai sepanjang length(x) atau length (n);
• K= k+1 adalah untuk pertambahan satu angka sehingga k selalu bertambah 
• Xe adalah untuk menampung nilai penjumlahan dari X yang berubah setiap perulangan 
• Figure;  untuk merepresentasikan dalam bentuk gambara/ 
• Subplot(4,1,2); untuk menempatkan gambar dalam satu bingkan dimana angka 4 menunjukkan banyak baris, 1 menunjukkan jumlah kolom, dan 2 menunjukkan posisi gambar. Dimana nilai-nilai ini dapat kita modifikasi sesuai keinginan 
• Abs, angle, real, imag sudah diterangkan di depan.

Contoh :

Kita punya x=[ones(1,4)]; dan n=[1:4];

Kemudian kita panggil fungsi yang telah kita buat tadi dan disimpan dengan nama DTFT. Panggil fungsinya dengan DTFT(x,n);

Dan hasil sinyalnya adalah seperti berikut ini :

Lanjut baca - Transformasi Fourier Waktu Diskrit (Discret-Time Fourier Transform)

Manipulasi Sinyal Diskrit Lanjutan

lanjutan dari praktikum kmarin tentang manipulasi sinyal diskrit

3. folding / Revers

Adalah operasi pembalikan dari sampel  x[ n] untuk mendapatkan sampel dengan urutan dilipat menjadi urutan y dilipat menjadi n.

Misalnya kita punya  x[n]={1,2,3,4,5,6,7,8,9}; -3<=n<=5

Jika dibalik maka  x[-n]={9,8,7,6,5,4,3,2,1};     -5<=n<=3;

Contoh di matlab :

x =[1:9]

x =

     1     2     3     4     5     6     7     8     9

n=[-3:5]

n =

    -3    -2    -1     0     1     2     3     4     5

Untuk membaliknya kita gunakan fliplr();

x2 = fliplr(x);

x2 =

     9     8     7     6     5     4     3     2     1

n2 = -fliplr(n);

n =

    -3    -2    -1     0     1     2     3     4     5

figure; subplot(2,1,1);stem(n,x);subplot(2,1,2);stem(n2,x2)

4. upsampling

Untuk menambahpanjang indeks, misalnya panjang indeks asalnya adalah 9, di up sebanya 3 indeks maka 3x9 = 27, maka setelah diupsampling maka panjangnya akan menjadi 27. Dan di setiap indeks disisipkan nilai 0 sebanyak 3-1=2 buah.

Dalam matlab fungsinya adalah menggunakan fungsi upsample

Syntax

upsample(x,n)

Y=upsample(x,n,phase)

>> x=[1:9]

x =

     1     2     3     4     5     6     7     8     9

>> k=3; // panjangnya adalah 9x3 dan angka 0 yang disisipkannya adalah k-1;

>> x2=upsample(x,k);

>> figure; subplot(2,1,1);stem(x);subplot(2,1,2);stem(x2)

5. downsampling

Downsampling merupakan kebalikan dari upsampling di akan mengurangi panjang indeksnya menjadi 9/3 = 3 dari semula. Jadi semisal panjang indeksnya 27 dengan di downsampling sebanyak 3 makan indeksnya akan menjadi 9 kembali dan sampelnya juga kembali lagi tanpa ada penyisipan angka 0.

Didalam matlab

Syntax

downsample(x,n)

Y=downsample(x,n,phase)

>> x=[1:9]

x =

     1     2     3     4     5     6     7     8     9

>> k=3;

>> x3=downsample(x2,k);

>> figure; subplot(3,1,1);stem(x); subplot(3,1,2);stem(x2)

subplot(3,1,3);stem(x3)

6. interpolasi

Iinterpolasi adalah manipulasi sinyal untuk meningkatkan rate oleh factor integer; mengestimasi nilai nilai diantara dua nilai.

Didalam matalab fungsinya adalah sebagai berikut.

Syntax

Y=interp(x,r);

Y=interp(x,r,l,alpha)

[Y,b]=interp(x,r,l,alpha)

X=[1:5,6:10];

X2=interp(X,3);

figure; subplot(2,1,1);stem(X);subplot(2,1,2);stem(X2)

7. scaling

Hal ini masing-masing sampel dikalikan dengan skalar, sehingga akan menghasilkan x[n] yang berbeda-beda untuk setiap perkaliannya.

Berikut ini adalah contohnya :

X=[1:5,5:-1:1]

a=2;a2=0.5;

>> x2=a.*X;

>> x3=a2.*X;

>> figure; subplot(3,1,1);stem(x2);subplot(3,1,2);stem(X);subplot(3,1,3);stem(x3)

DERET FOURIER

Adalah deret  sinyal yang dihasilkan oleh sinyal sinusoidal.

Dengan matlab kita bias membuat deret ini seperti dibawah ini. Pertama adalah>> t=-3:0.01:3;

>> a0=0.5.*ones(1,length(t));

>> figure;plot(t,a0);

Ini untuk sampel 0,5 dari -3 sampe 3 gambarnya seperti dibawah ini

>> s2=2/pi*sin(pi.*t);

figure;plot(t,s2)

hasilnya adalah

>> s3=2/(3*pi)*sin(3*pi.*t);

figure;plot(t,s3)

hasilnya adalah

>> s4=2/(5*pi)*sin(5*pi.*t);

figure;plot(t,s4)

hasilnya adalah

 

 Jika semua hasil tadi di jumlah maka akan menjadi seperti gambar berikut ini.

stotal=a0+s2+s3+s4;

figure;plot(t,stotal);

Atau untuk jika kita ingin menjadi kan dalam satu table berikut adalah hasilnay

stotal=a0+s2+s3+s4;

figure;subplot(5,1,1);plot(t,a0);subplot(5,1,2);plot(t,s2);subplot(5,1,3);plot(t,s3);subplot(5,1,4);plot(t,s4);subplot(5,1,4);plot(t,stotal);

Jika kita ingin menghitung lebih dari 4 kali maka kita menggunakan looping agar dapat dilakukan dengan mudah dan cepat, misalnya penghitungan dilakukan sebanyak 19 kali maka hasilnya akan seperti dibawah ini:

Syntax :

t=-3:0.01:3;

h=19; // semakin maka akan semakin siku

a0=0.5.*ones(1,length(t));

for n=1:2:h

sn=2/(pi*n)*sin(n*pi.*t);

sinyaltotal=sinyaltotal+sn;

end

figure;plot(t,sinyaltotal)

Lanjut baca - Manipulasi Sinyal Diskrit Lanjutan